در این مقاله قصد داریم درمورد الگوریتم دیکسترا کوتاهترین مسیر صحبت کنیم و این الگوریتم را به صورت گام به گام توضیح داده و همراه با رسم شکل مراحل آن را بررسی کنیم. پس اگر علاقمند به یادگیری این الگوریتم هستید در ادامه با ما همراه باشید.

مقدمه الگوریتم دیکسترا کوتاهترین مسیر

الگوریتم دیکسترا (Dijkstra’s Algorithm) یا اولین الگوریتم کوتاهترین مسیر دیکسترا (Dijkstra’s Shortest Path First) از جمله الگوریتم‌هایی است که برای پیدا کردن کوتاهترین مسیر از گره آغازین تا گره هدف در گراف وزن دار (گرافی هست که یال‌های آن دارای وزن هستند) استفاده می‌شود.

الگوریتم دیکسترا یا دایجسترا (که البته درست آن دیکسترا هست ولی خوب دایجسترا هم بهش گفته می‌شود) الگوریتمی برای پیدا کردن کوتاهترین مسیر بین گره مبدا و دیگر گره ها در یک گراف است که البته از آن برای پیدا کردن کوتاهترین مسیر بین دو گره هم استفاده می‌شود. این الگوریتم اولین بار توسط یک دانشمند هلندی به نام ادسخر ویبه دیکسترا (Edsger Wybe Dijkstra) معرفی شد و بعد از حدوداً سه سال منتشر شد.

الگوریتم دیکسترا کوتاهترین مسیر، یک درخت از کوتاهترین مسیرها، که از رأس شروع شده تا نقاط دیگر گراف ادامه دارد، ایجاد می‌کند. تصور کنید در نقطه‌ای از شهر قرار دارید و یک قرار کاری بسیار مهم در نقطه دیگر شهر دارید و عجله می‌کنید که سر وقت به قرارتان برسید. حالا اگر برای یافتن مسیرهایی با کوتاهترین مسافت یا به عبارتی کمترین ترافیک روی نقشه بگردید به نحوی از الگوریتم دیکسترا استفاده کردید.

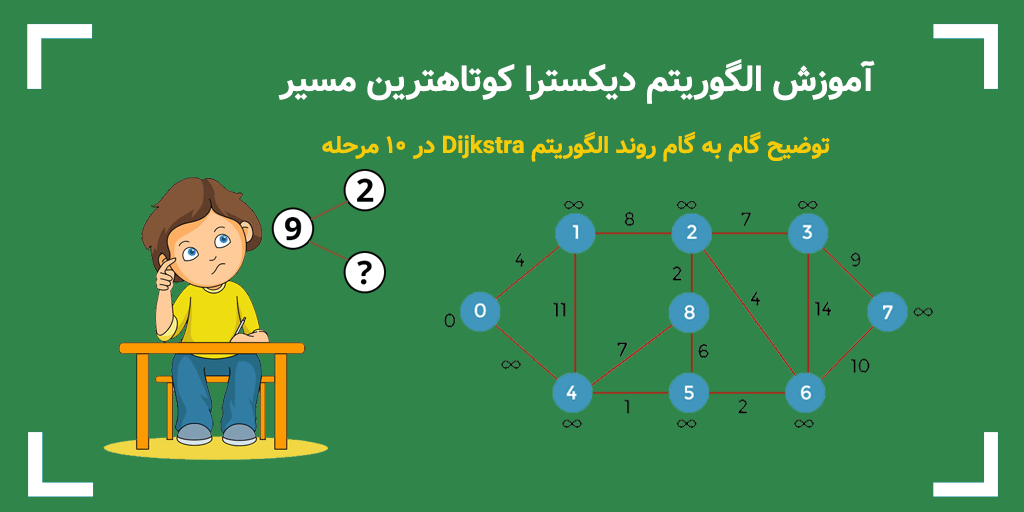
در این الگوریتم وزن‌های بر روی یال‌ها همان ترافیک خیابان یا مسافت طی شده برای گذر از آن خیابان را نشان می‌دهند. شکل زیر یک گراف را با تعدادی رأس و یال‌های وزن دار آن نشان می‌دهد.

نحوه کار الگوریتم دیکسترا کوتاهترین مسیر

نحوه کار این الگوریتم به این شکل است که در ابتدا یکی از رأس ها به‌عنوان رأس مبدأ انتخاب می‌شود. سپس گره‌های همسایه آن در نظر گرفته می‌شوند. گره‌ای که از گره مبدأ با کمترین وزن قابل دسترسی هست به عنوان گره بعدی انتخاب می‌شود و در نهایت به محض پیدا شدن کوتاهترین مسیر از مبدأ به مقصد الگوریتم متوقف می‌شود.

این الگوریتم از طرفی شبیه الگوریتم پریل هست و اگر وزن یال‌ها منفی باشد درست کار نخواهد کرد در این صورت از الگوریتم‌های دیگری مثل الگوریتم بلمن فورد می‌توان به جای آن استفاده کرد البته پیچیدگی بالاتری دارد.

روند کار الگوریتم دیکسترا کوتاهترین مسیر

روند کار این الگوریتم دارای چندین مرحله است:

• در اولین مرحله یک رأس یا گره به عنوان گره مبدأ انتخاب می‌شود که وزن آن گره در ابتدا برابر صفر است.
• در مرحله بعدی همسایگان آن گره که مسیری به گره مبدأ دارند مورد بررسی قرار می‌گیرند. هر کدام که وزن مسیر کمتری داشته باشد به عنوان گره بعدی انتخاب می‌شود و وزن مربوطه بر روی گره مد نظر نوشته می‌شود که این وزن از جمع وزن مسیر طی شده از مبدأ تا گره مد نظر محاسبه می‌شود و گره‌هایی که خارج از محدوده هستند تا زمانی که پیمایش نشدند وزن بی‌نهایت دارند.(در ادامه با توضیح از طریق شکل‌ها بهتر متوجه خواهید شد.)
• مجموعه S را اگر مجموعه گره‌های مشاهده شده در نظر بگیریم هر گره پیمایش شده در آن قرار می‌گیرد و به نحوی مسیر پیمایش شده از مبدأ تا مقصد از طریق آن قابل مشاهده خواهد بود و این کار را ادامه می‌دهیم تا همه گره‌ها پیمایش شوند. در پایان اگر گره مقصد دارای اندیس یا همان وزن باشد. آن عدد نشان دهنده مسافت بین مبدأ و مقصد است.

همچنین برای پیدا کردن مسیر می‌توان اندیس دیگری برای هر گره در نظر گرفت که نشان‌دهندهٔ گره قبلی در مسیر طی شده باشد. بدین ترتیب پس از پایان اجرای الگوریتم، با دنبال کردن گره‌های قبلی از مقصد به مبدأ، کوتاهترین مسیر بین دو نقطه نیز یافت می‌شود.

در حین اجرای الگوریتم دیکسترا کوتاهترین مسیر، دو مورد نگهداری می‌شود. یکی مجموعه s از گره‌هایی که وزن کوتاهترین مسیر از مبدأ تا آنها مشخص‌شده و پیمایش شده‌اند و بعدی دنباله d که برای هر گره v بصورت dv که برای نشان دادن کوتاهترین مسیر از مبدأ تا گره v هست. به‌شرطی که تمام گره‌های این مسیر به‌جز خود گره v جزئی از مجموعه s باشند.یعنی قبلاً به دلیل کوتاهترین مسیر بودن پیمایش شده‌اند.

مقدار اولیه s تهی هست و مقدار d برای همه گره‌ها در ابتدا به‌جز آنهایی که مستقیماً به گره v (مبدأ) وصل هستند بی نهایت است. الگوریتم در هر مرحله گرهی را که خارج از مجموعه s هست و d آن به عبارتی وزن مسیر آن کمترین هست انتخاب کرده و داخل s قرار می‌دهد سپس مقادیر d را برای گره‌های همسایه بروز می‌کند چون پیمایش گره جدید مسیرهای جدیدی را تا مقصد برای گره مبدأ باز می‌کند.

کاربردهای الگوریتم دیکسترا کوتاهترین مسیر

از جمله یکی از مهم‌ترین کاربرهای الگوریتم دیکسترا کوتاه‌ترین مسیر، می‌توان به محاسبه کوتاه‌ترین فاصله دو نقطه در یک شهر را مثال زد که بالا اشاره کردیم. نقاط مورد نظر را روی نقشه پیدا می‌کنیم. با استفاده از مشخصات نقاط (طول و عرض و ارتفاع) فاصله نقاط را در هر عملیات حساب می‌کنیم. حالا فرض کنیم اگر ملاک محاسبه را طول مسیر در نظر بگیریم در مواقعی که ترافیک شدید داریم فرضاً راهی داریم از اتوبان و نسبت به راه درون‌شهری دیگر طولانی‌تر ولی درون‌شهری ترافیک سنگین دارد با وجود طولانی بودن مسیر ترافیک در اتوبان انتخاب اتوبان باعث می‌شود سریع‌تر به مقصد برسیم.

در این موارد می‌توان کاهش سرعت را با افزایش فواصل هم‌ارز نمود چراکه اگر رابطهٔ سرعت و فاصله را خطی در نظر بگیریم D= V.T تأثیر کاهش سرعت و افزایش مسافت یکسان خواهد بود. بنابراین می‌توان یکسری ضرایب تعدیلی در فواصل بین نقاط ضرب کرد و بدین گونه در محاسبات لحاظ کرد. از جمله مهم‌ترین این ضرایب می‌توان به ۱- ضریب ترافیک و شلوغی ۲- ضریب عرض معبر ۳- ضریب شیب که نشانگر افت سرعت در سربالایی ها است اشاره کرد.

اگرچه تعیین این ضرایب نیاز به افراد متخصص در زمینه ترافیک و.. دارد ولی می‌توان انتظار داشت که در بیشتر مواقع این ضرایب بین 1 تا 2 بسته به شرایط تغییر کنند.

سخن آخر در مورد الگوریتم دیکسترا کوتاهترین مسیر

اگر تا انتهای مقاله با ما همراه بودید متوجه شده‌اید که الگوریتم دیکسترا کوتاهترین مسیر یا دایجسترا الگوریتمی هست بسیار کاربردی به خصوص در مسائلی همچون پیدا کردن کوتاهترین مسیر بین دو نقطه که این دو نقطه می‌تواند بین دو شهر، دو منطقه و … باشد. با کمک این الگوریتم می‌توانیم چندین نقطه را با عبور از کوتاهترین مسیرها پیمایش کنیم یعنی کوتاهترین مسیر بین یک نقطه و بقیه نقطه‌ها را پیدا کنیم.

همچنین در این مقاله مراحل این الگوریتم به‌صورت گام‌به‌گام همراه با رسم شکل و توضیحات لازم بیان‌ شده است. امیدوارم از مطالعه این مقاله لذت برده باشید و برایتان کاربردی بوده باشد.